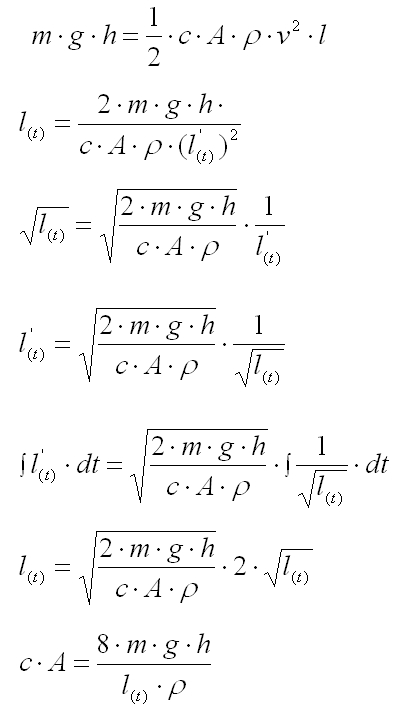Egy vargabetű és egy vallomás

 3. rész

Eltérve az eredeti témától, az úszás közben fogyasztott energia kiszámításától egy vargabetűt teszek az előző részben tervezett fordulónál ajánlott siklási távolság kiszámítása céljából. Ellentétben az eredeeti témával ennek gyakorlati haszna is van.

A számítások célja a következő képpen fogalmazható meg:
Ismerve az úszási sebességét a versenyzőnek, meghatározható az a maximális távolság, amelynél a vízalatti siklás sebessége megegyezik az úszás sebességével, amikor is érdemes felszínre jönni, hogy ne kelljen az úszó testét újra gyorsítani. Ez egy elméleti érték és függ a forduló technikai kivitelezésétől valamint attól, hogy a víz alatt tartózkodás idején fellépő légszomj később hátrányos lehet ami igaz a következő megjegyzés esetén is.

Megjegyzés: A valóságban a rajt és fordulók szabályai miatt az úszó mellúszásnál egy teljes tempót tehet a víz alatt, egy delfin lábtempóval, a következő kéztempó befejezése előtt át kell törje a feje a vízfelszínt. A gyors, hát, pillangó úszásnemeknél a víz alatti delfinezés megengedett maximum 15 méterig.

Az előző részben tárgyalt számítás esetén végzett méréseket kellene elvégezni:
  • megmérjük mekkora az emelkedés helyből felugrásnál
  • megmérjük a faltól elrúgva magát, meddig siklik az úszó, kar és láb segítsége nélkül
  • ismerve az úszó test tömegét kiszámítható mekkora az A*c értéke

Az ajánlott siklási táv kiszámítása fordulónál

Amikor helyből felugrunk úgy, hogy súlypontunk "h" magasságra emelkedik a helyzeti energiánk W=m*g*h [Joule] (ahol m a test tömege, g=9,81 m/s2 a garvitációs gyorsulás, h pedig az emelkedés).

Az elugrást félig guggoló helyzetből végezzük éppen úgy ahogy a vízben a faltól elrugaszkodunk. Ezt az utat "s" -el jelölve azt jelenti, hogy a test álló, helyzetből indul, tehát az elugrás pillanatában 0 a sebessége, majd az földtől való elszakadás pillanatában a legnagyobb a sebesség. Ez a sebesség levegőben alakul ki, tehát a testre elhanyagolható mértékben hat a közegellenállás, de hat a gravitáció. A vízben más a helyzet, mert a gravitációt csökkenti a felhajtó erő (az sem az elmozdulás irányában hat), de nagyobb a közegellenállási erő (a víz 800 szor sűrűbb a levegőnél) és ez az erő a sebesség négyzetével egyenes arányban nő.

Az erő, amelyet kifejtünk az elrugás ideje alatt a W=F*s ből számítható ki. Vagyis F=(m*g*h)/s [N].

Ezekből az adatokból jó becslés adható, mekkora a közegellenállás (vagyis az A*c szorzat) úszás közben és kiszámítható az ajánlott siklási hossz mégpedig a mellékelt képlet alkalmazásával.
Figyelem! Az időt másodpercben az úszott távolságot méterben kell megadni. Tehát pl. egy óra helyett 3600 másodpercet írunk.

Emelkedés: méter    
Test tömege: kg    
Testmagasság: méter    
Siklás: méter    
Úszott táv: méter Adott úszásnemben elért idő: mp
 
Ajánlott siklási hossz a faltól: méter

A fenti számításban használt értékeket mindenki könnyen megmérheti/megbecsülheti saját maga számára. Érdekelne a tapasztalatotok és az általatok mért adatok.

A II. rész számításának kritikája. Vallomás.

Az első írásom után, Dr. Batta Gyula úszótársunk, írt egy levelet, amelyben a biofizikai mérések alapján megerősítette, hogy a 10% os fizikai munkából számított érték bizony lehet helyes. A maradék 90%-ra nincs pontosan számítható magyarázat.

A levélben a következőket írta:

  1. A biofizika tankönyvben a következő szerepel:
    Az alapanyagcserénkre kb. 71 kcal/h energiát kell fordítanunk. Folyamatos (feltehetően F*s típusú mechanikai, 10h), munkavégző képességünk 65 kcal/h (kb 75W).
    Tehát a hatásfokunk így durván 50%, ami sokkal jobb mint a gőzgép vagy a benzinmotor (lásd mátrix c. film)
  2. A maratoni úszónál a zsírvesztés, izomvesztés és energiapótlás összegéből 11750 kcal energia adódik, ami az időt (8h52) figyelembe véve 1325 kcal/h. Az 50% hatásfok miatt ebből marad 663 kcal/h. Ha ennek is a tizedét veszem, akkor kapom a tankönyvi 66 kcal/h értéket a mechanikai munkára. Az általad számolt úszási mechanikai munka pedig 79 kcal/h.
  3. Hol van a deficit?
    1. a mechanikai munka kiszámítása a közegellenállás erejével szemben egy passzív (mozdulatlan, nincs karmozgás, stb.) úszót feltételez egy áramlási csőben
    2. a kar és lábmunkát végző aktív úszó irdatlan mennyiségű víztömeget gyorsít fel nulláról.
    3. A 22 C hőmérsékletű víz áramlása jelentős hőenergiát visz el igen hatásosan a 37 C hőmérsékletű testről.
    4. a biokémiai hatásfok lehet hogy romlik nagyobb teljesítményeknél (pl a szívfrekvencia emelkedése miatt).
Tehát a stílus és az eredményesség korrelál, lásd azokat az úszótársakat, akik nagyon jól úsznak és nem izomkolosszusok.

Érdekes lenne futóknál hasonló vizsgálat, hiszen ott nincs víztömeg.



Sajnos egy vallomással tartozom az úszótársaknak. A II. részben a számításban egy hibát követtem el.
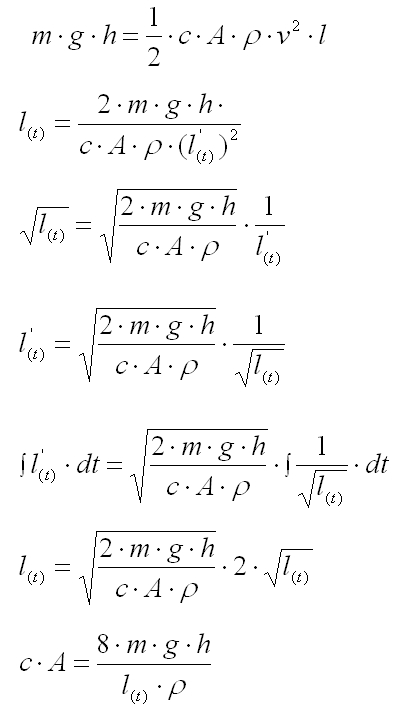
A műegyetemen a diák humorhoz tartozott a "Johnson féle állandó". Johnson féle állandónak neveztük azt a számot, amellyel szorozzuk vagy osztjuk az eredményt vagy amelyet kivonjuk illetve hozzá adjuk az eredményhez abból a célból, hogy a várt eredményt kapjuk. Az én Johnson féle állandóm éppen tíz volt. Azaz csak 4,19*100 al osztottam 4,19*1000 helyett, amikor kcal-át számoltam joule-ból.

Az eredeti képlettel ugyanazt az eredményt kaptam mint, ami a biofizikai tankönyvekben szerepel és amit az első részben számítottam ki. A tízszeres szorzónak hála, bár csak tizede a számolt fizikai munka, az energia fogyasztás becslése közelít a svájci úszótársak mérési eredményéhez (lásd első rész), de ennek nem sok köze van az általam (a mellékelt levezetéssel) "tudományosan" kiszámított értékhez.

A becslés a számítás és a tankönyv által adott számítható 10% on belül valószínűleg helyes lesz és ezért a tízszeres szorzat is közel lesz a valósághoz. A különbségeket ugyanakkor megnöveli.



2010. június 16.
írta Miklós Attila